心拍や呼吸等のバイタルサインによるミリ波帯の位相変化の解析
人体モデルとレーダー
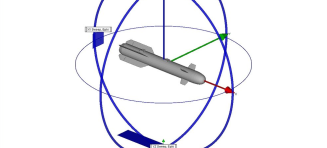
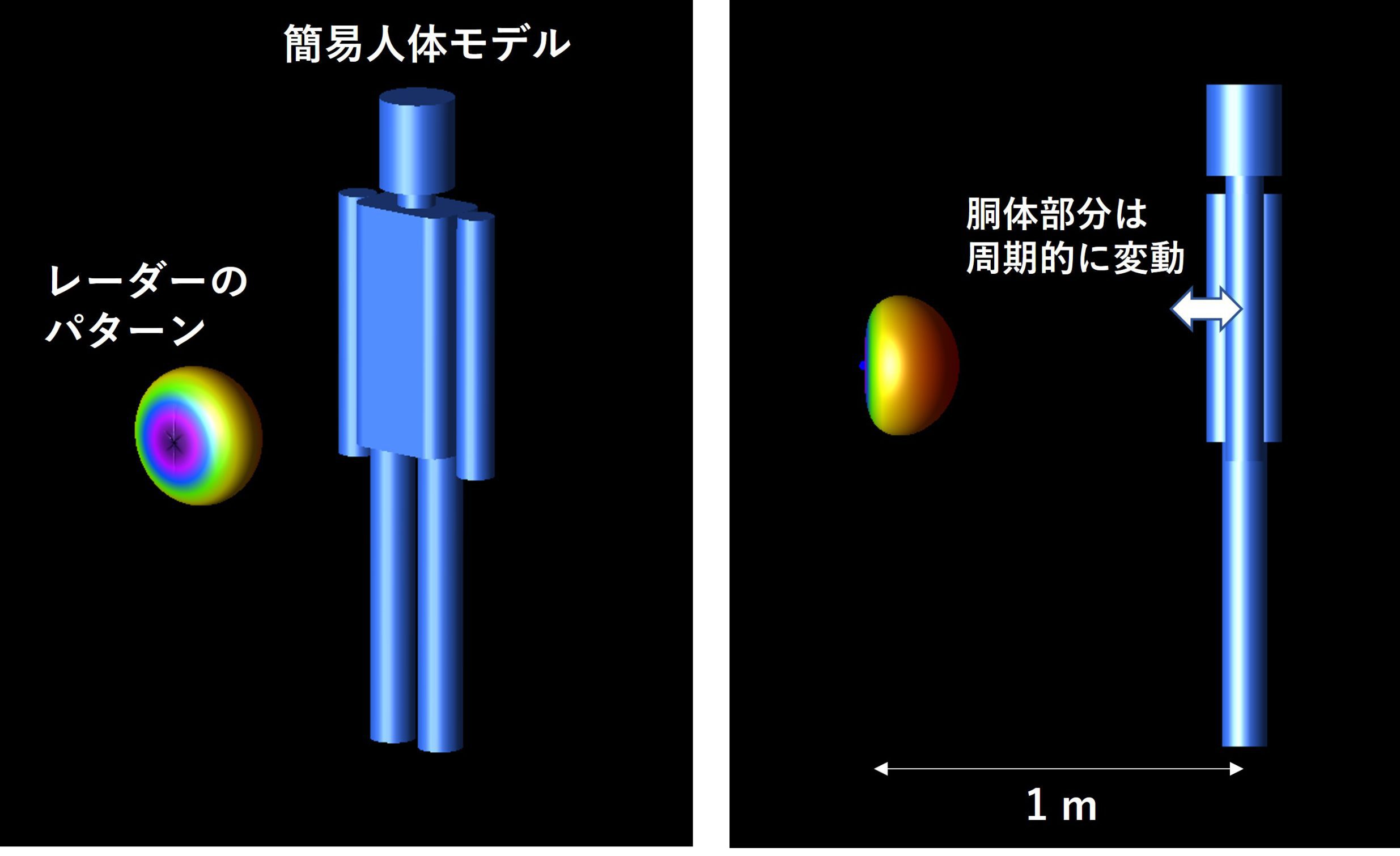
- 人体モデルは、図のような簡易形状のモデルを使用する。
- レーダーの放射パターンは人体方向に指向性を持つように設定し、周波数は2.4GHz、24GHz、60GHzの3つとする。
- 人体モデルの胴体部分の寸法は、呼吸と心拍により周期的に変動するようにパラメータを設定する。今回は、呼吸のみの変動を与えたモデルと、心拍のみの変動を与えたモデルの2種類を用いる。
呼吸と心拍による周期的な変位のモデル化
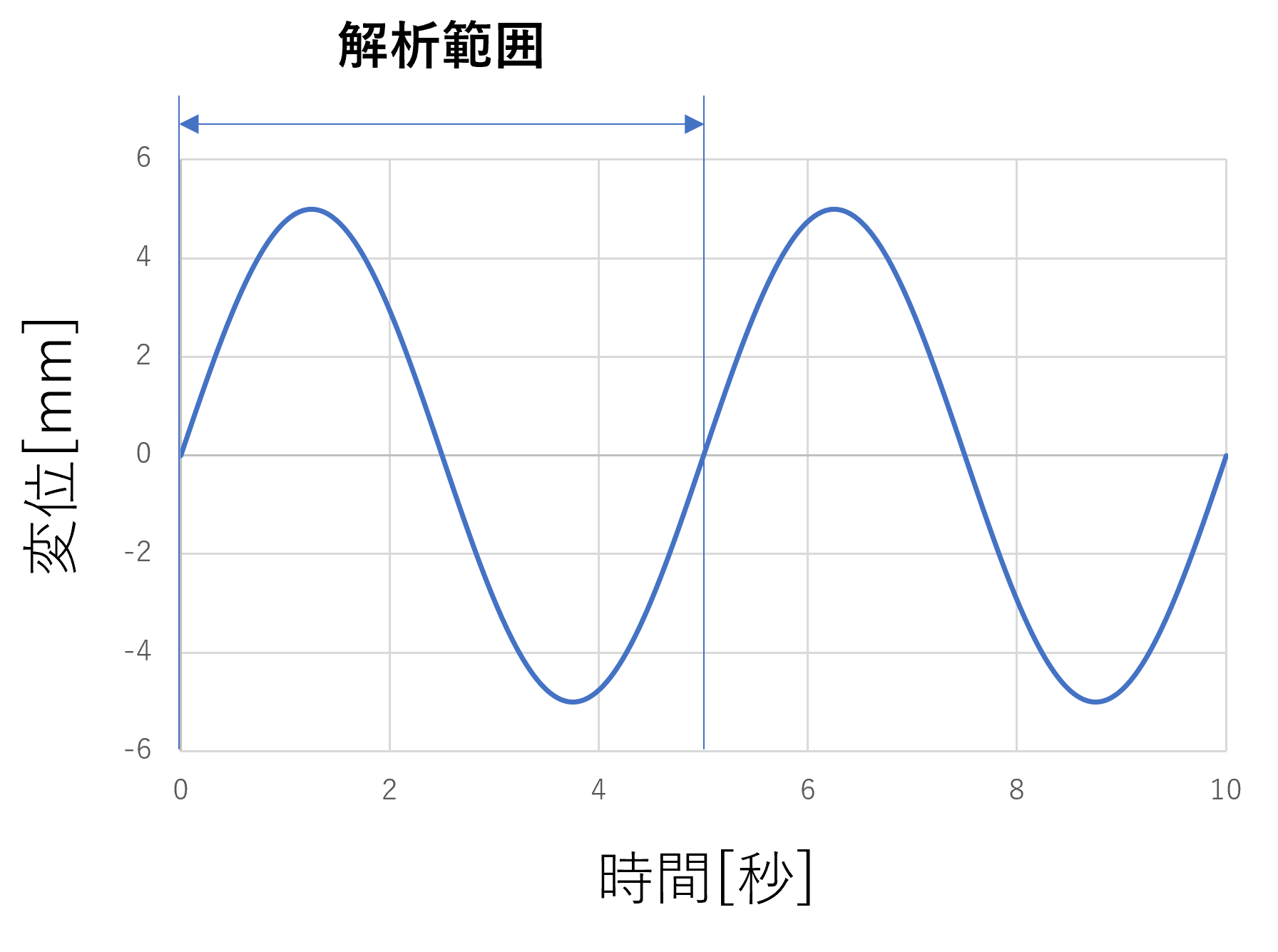
- 人の呼吸による体動は比較的滑らかで正弦波に近いと仮定し、変位としては周期5秒で振幅が5mm（peak-to-peakで10mmの変位）のsin波（下図）を設定する。
- 解析する範囲は1周期分（0～5秒）とし、刻み幅は0.01秒で計500回の計算を実施する。0.01秒ごとに人体モデルの寸法が与えられた変位パラメータに従って微小変化することになる。
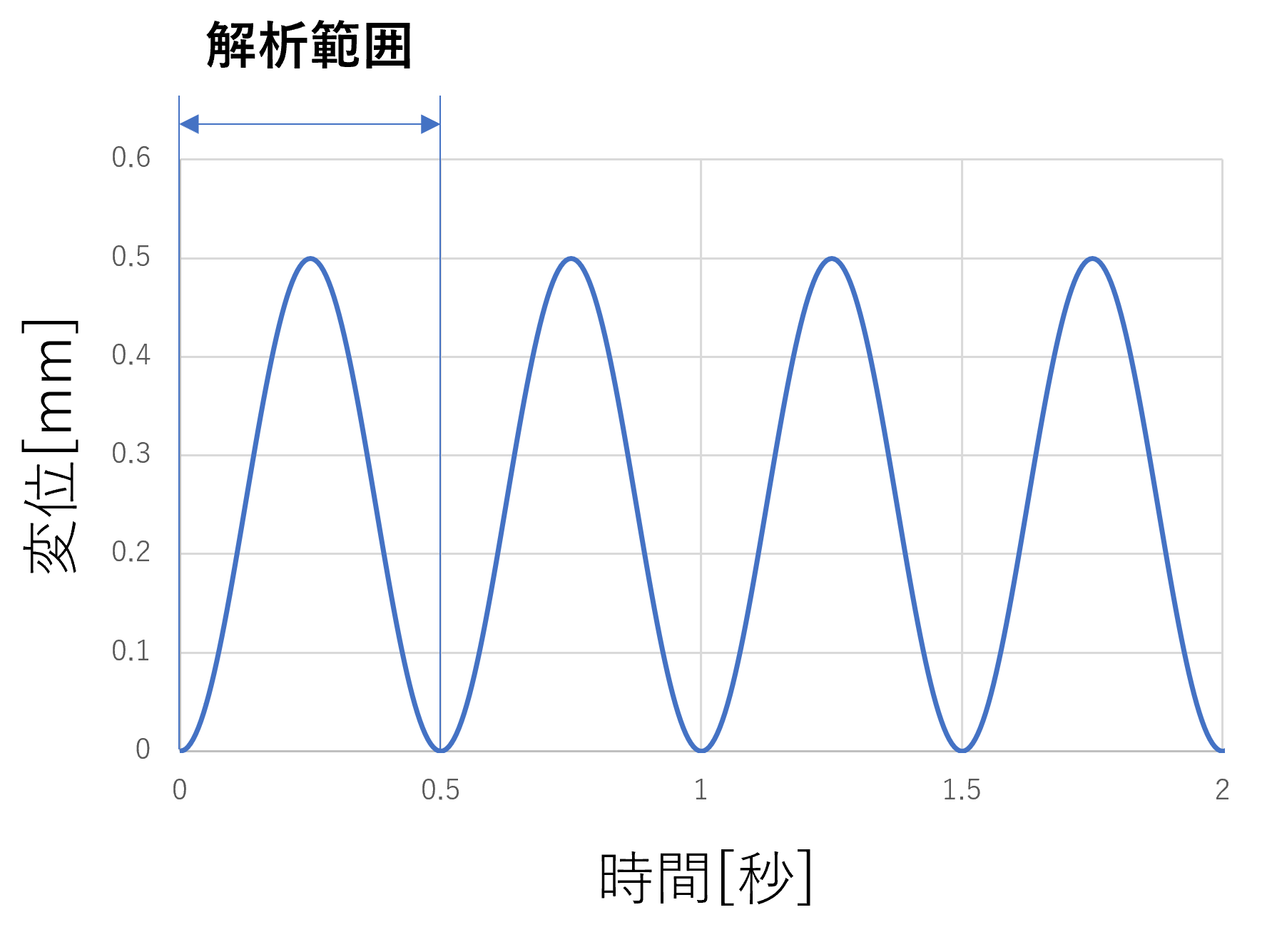
- 一方、心臓の拍動（心拍）は正弦波的ではなくパルス状に近いと仮定し、変位としては周期1秒のsin波を2乗したものを最大振幅0.5 mmとなるように設定する（下図）。これは、peak-to-peakで0.5mmの変位量となる。
- 心拍の変位を与えたモデルの解析範囲は0～0.5秒とし、刻み幅は0.001秒で同じく計500回の計算を実施する。
位相変化をみるパスの抽出
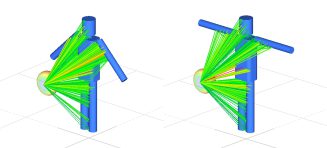
- 計算結果の一例の伝搬経路（パス）を可視化したものが下図（左）である。なお、パスの色はそれぞれの伝搬経路での受信電力強度を表している。
- 今回のモデルで呼吸と心拍によって微小変位しているのは胴体部分のパーツのみであるため、それ以外のパーツからのパスの受信電力や位相には時間依存性が基本的には無いと考えられる。そのため、呼吸や心拍の変位の影響のみを確認するために胴体パーツから反射されたパスのうちで最も受信電力が大きいパス（下図の右）のみを抽出し、このパスの位相変化を求める。
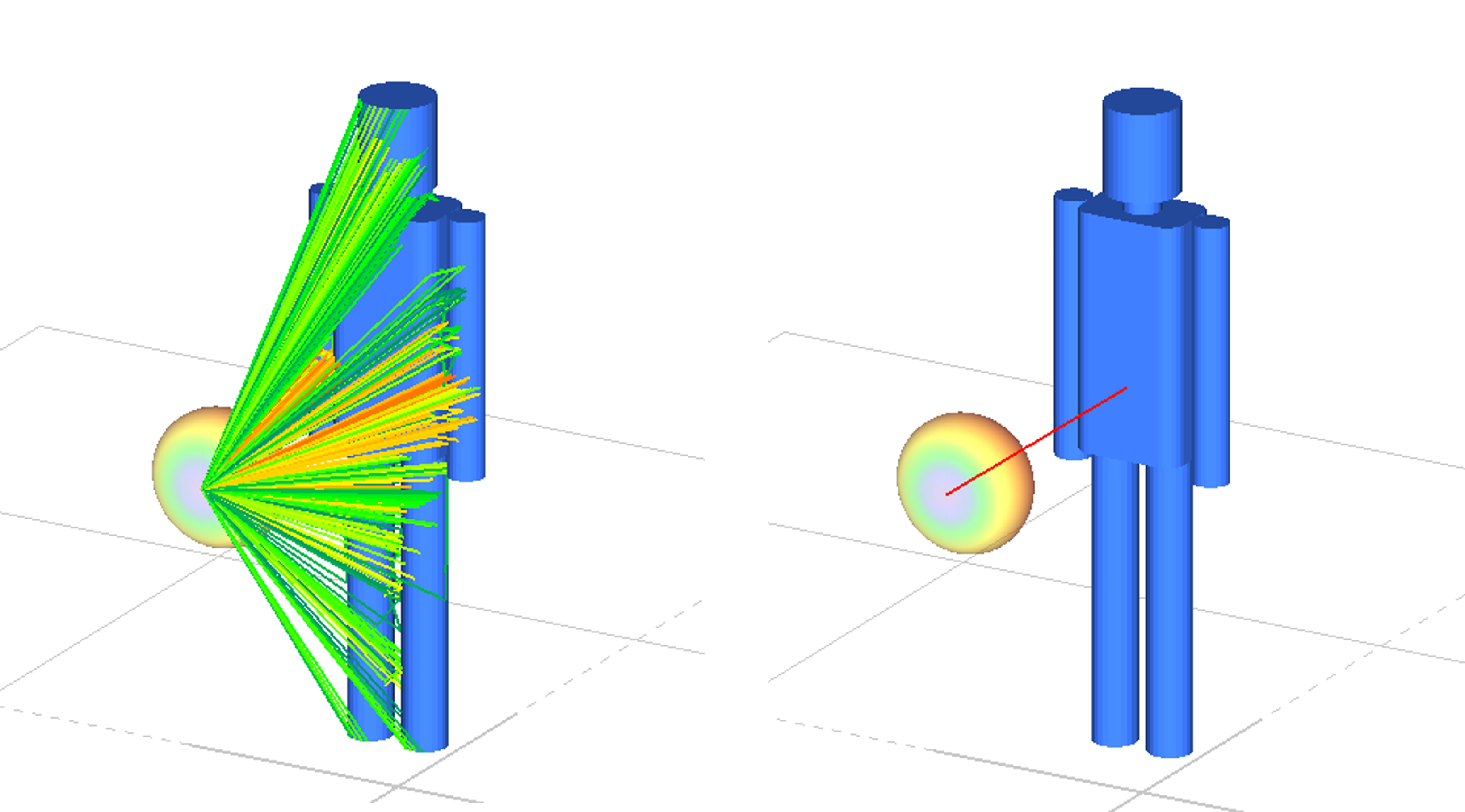
（左）胴体以外のパーツからの反射も含めたパスの様子 （右）胴体からの反射で最も受信電力が大きいパス
周波数による位相変化の違い
- まず、呼吸による変位（Peak-to-peakで10mm）のみを与えた人体モデルに対する位相変化を示す。これは、解析結果として得られた位相（各500個）を実部成分と虚部成分で複素平面上にプロットしたものであり、位相変化の軌跡は円を描くこととなる。なお、振幅の最大値が1となるように正規化している。
- この時の位相変化の軌跡は、モデルの微小変位に対応した角度範囲の円弧（場合によっては円）を描くことになる。この円弧の角度範囲は、周波数とモデルの微小変位量に依存する。周波数が低く変位も小さければ位相変化はほとんどなくなり、円弧は短くなる。逆に周波数が高く変位も大きければ位相変化が大きくなり、円弧も長く（長すぎると一周して円に）なる。
- WaveFarerの解析では振幅と周波数が一定の連続波（CW波）を基本としており、このプロット上の円弧の角度範囲はCWレーダーの受信信号を直交検波して描画したI-Qプロットのそれに相当すると考えられる。
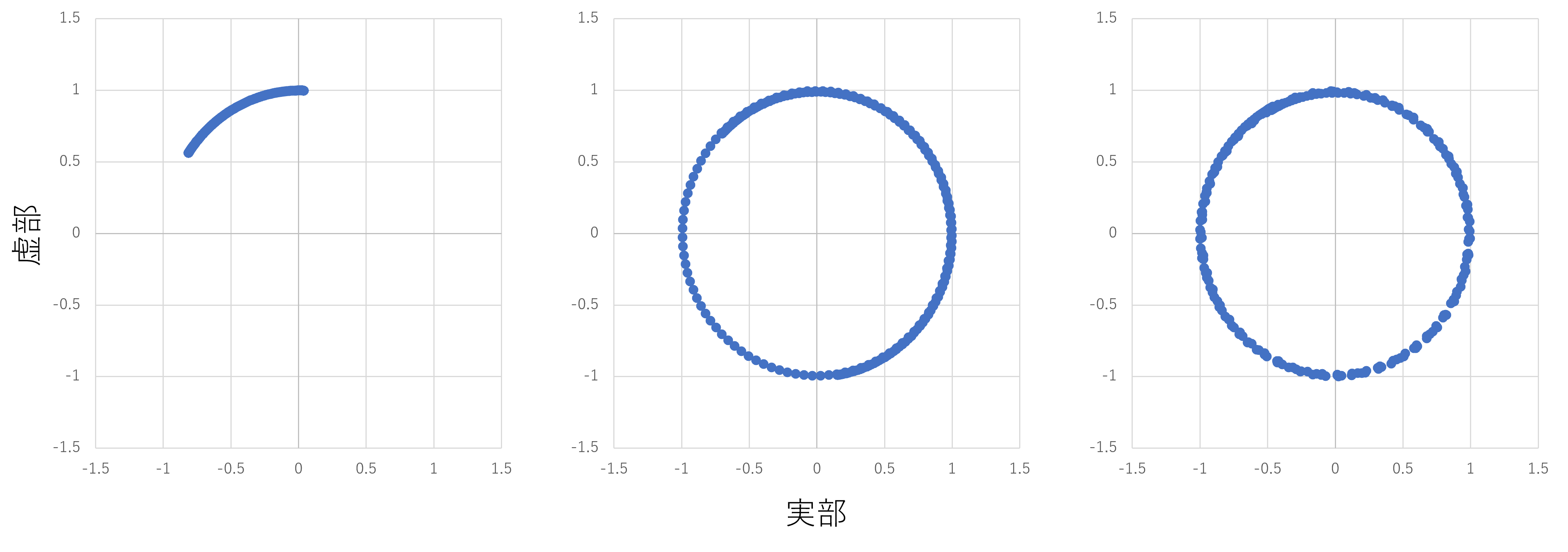
呼吸による変位が反映された周波数毎の位相の軌跡（左から、2.4GHz、24GHz、60GHz）
- この結果から、呼吸による変位（Peak-to-peakで10mm）は、2.4GHzでおおよそ60度の位相変化として観測できることが示される。一方で、24GHz、60GHzという高い周波数帯になると、10mmの変位は波長に対して大きくなり、位相変化は360度を超えて複素平面上では円としてプロットされる。
- 次に、心拍による微小変位（Peak-to-peakで0.5mm）のみを与えた人体モデルに対する位相変化を同様の形式で示す。
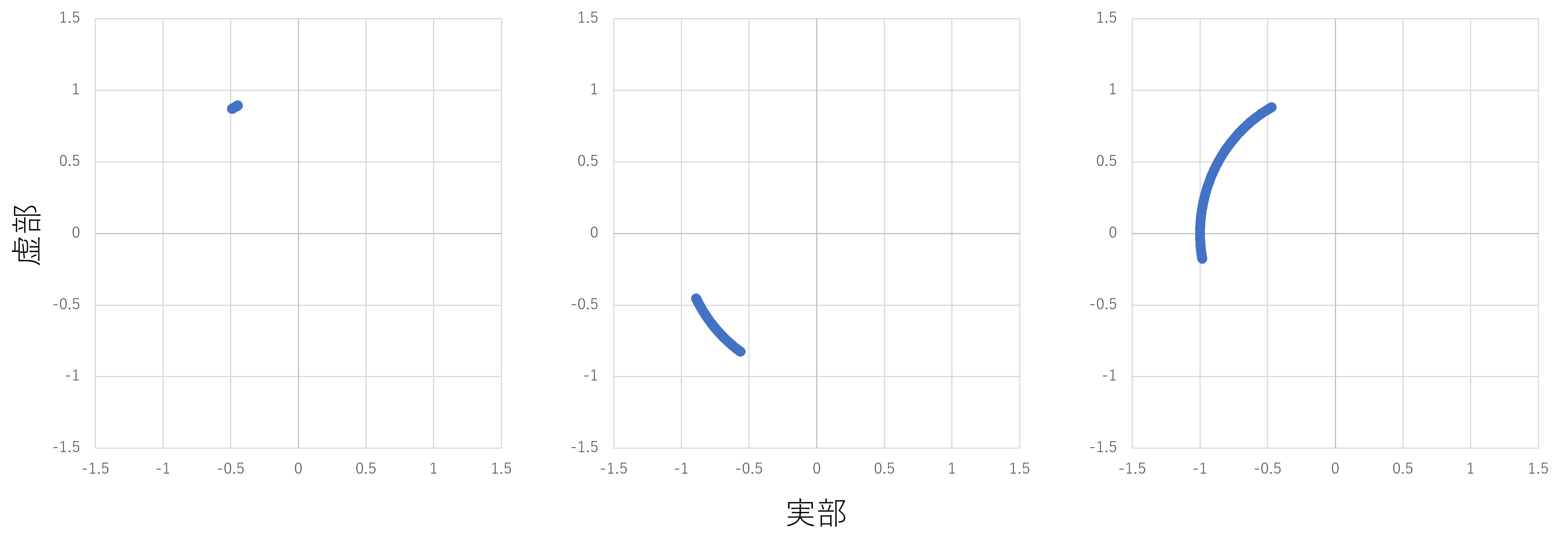
心拍による変位が反映された周波数毎の位相の軌跡（左から、2.4GHz、24GHz、60GHz）
- 心拍による変位はPeak-to-peakで0.5mmと呼吸に比べて1/20と小さいため、波長の長い2.4GHzでは位相変化も小さく点のようなプロットとなっている。
- 一方で、24GHz、60GHzでは波長の短さからある程度大きな位相変化を確保することができており、24GHzでは約30度、60GHzでは約60度の円弧となっている。このことは、高い周波数を使用することで心拍による人体の微小変位をある程度大きな位相変化として捉えることが可能であることを示唆している。
マルチパス環境下での位相変化について
- ここまでは人体モデルのみを考慮していたが、実際の環境では床や壁などの反射によるマルチパスが存在する。例えば、以下のように床と壁を加えたモデルを考える。このモデルでは、解析周波数は24GHzで人体モデルに与える変位は呼吸のみ（Peak-to-peakで10mm）とし、床と壁の材質は完全導体とする。
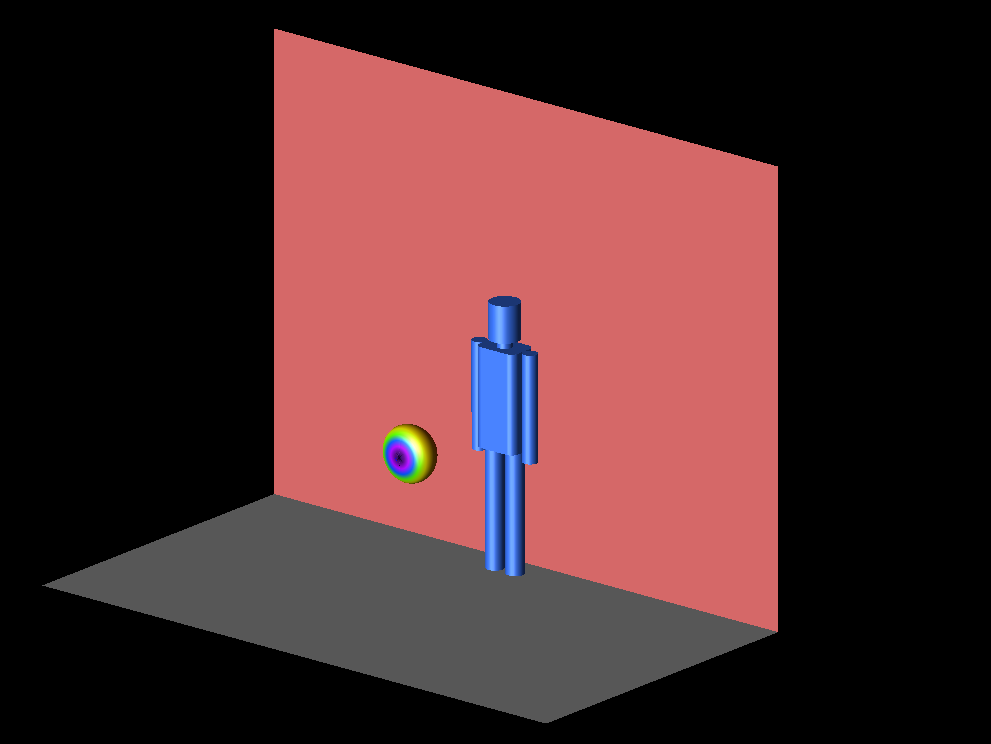
- このモデルの解析結果は、マルチパスの影響を含めるために全てのパスを合計した受信信号の位相変化とする。位相変化の軌跡を同様にプロットしたものを以下に示す。
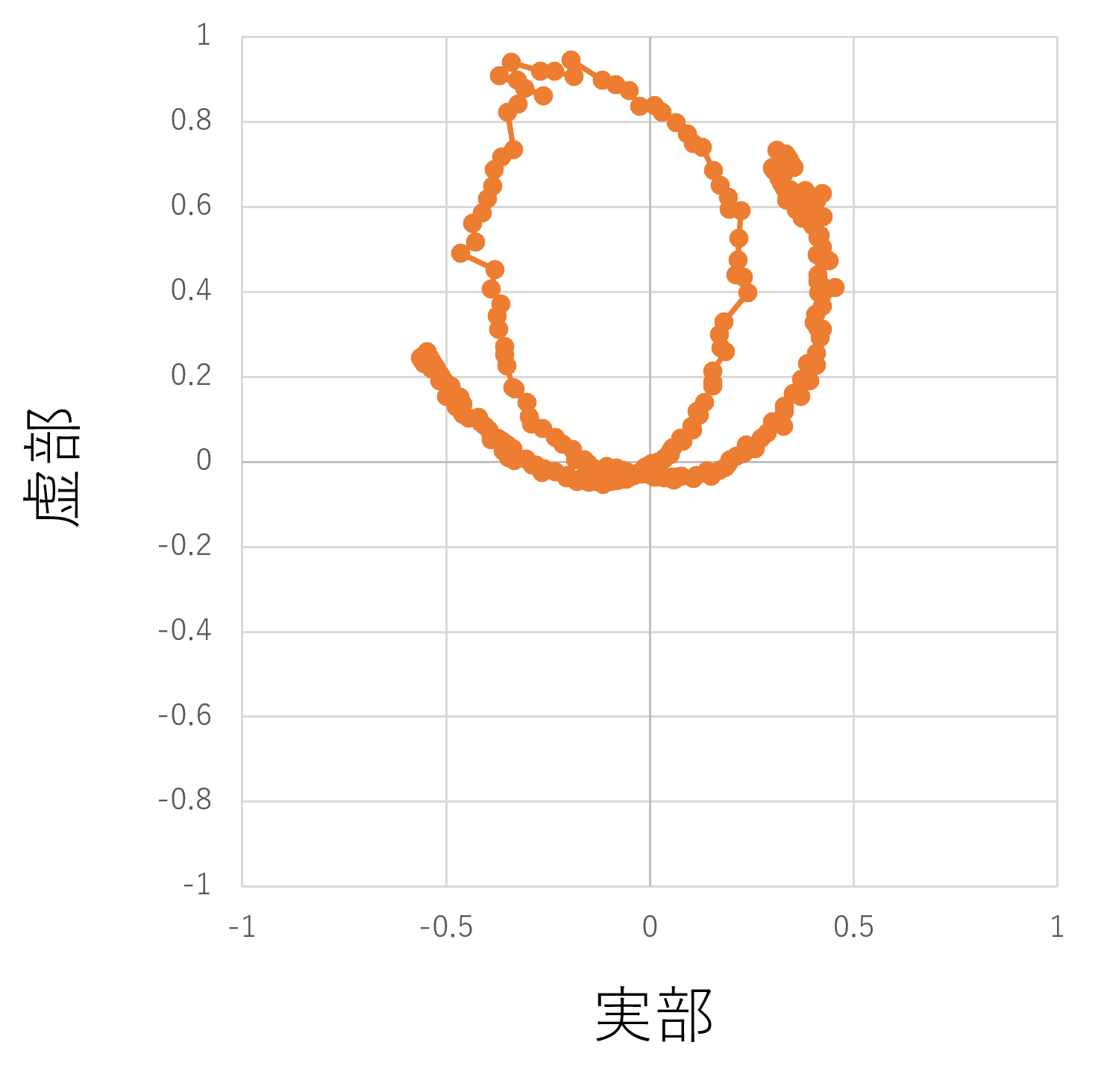
- 時間変化しないオブジェクトからのパスは位相の変化がないため、それらを含んだ受信信号の位相変化の円弧の中心は複素平面上の中心点からずれていることが確認できる。また、マルチパスの中にも呼吸による変位の影響を受けているパスも混ざることで少し歪な円を形成していることがわかる。
- なお、呼吸による変位（Peak-to-peakで10mm）に対する24GHzの位相変化は計算上では約575度となる。グラフ上で描かれた円弧はおおよそ一周半以上の軌跡を持っており、この値とも一致する。
まとめ
- 呼吸と心拍それぞれの変位を人体モデルに与え、ミリ波帯までの3つの周波数（2.4GHz、24GHz、60GHz）における位相変化を WaveFarer を使用して解析した。
- 得られた位相を実部と虚部の複素平面上にプロットすることで、呼吸と心拍それぞれの変位に対応する円として描画した。結果として、今回のモデルに与えた呼吸の変位（Peak-to-peakで10mm）は2.4GHzの周波数で位相変化が約60度となり、ミリ波帯を使わずとも計測可能であることが示唆された。一方、心拍の変位（Peak-to-peakで0.5mm）は24GHzや60GHzの高い周波数を使用することで約30～60度の位相変化となることが確認できた。
- 本稿では理想的なパスを抽出して位相変化を確認したが、実環境では人体モデル以外からのマルチパスの影響が含まれる。WaveFarerでは、これらのオブジェクトもモデル化することでその影響を確認することができる。
